Table of Contents
Sverdrup Relation
Author: Natalie Kuster, Roland Häberli
The Sverdrup relation is a theoretical relationship between the wind stress exerted on the surface of the open ocean and the vertically integrated meridional (north-south) transport of ocean water. — Wikipedia 2014/04/22 11:32
Physical Concept
Physical explanation for the Sverdrup relation is that in the ocean interior away from the surface, vorticity is produced by vortex stretching.
The Sverdrup balance is saying that the meridional transport of the entire water column is directly related to and totally determined by the curl of the windstress. In other words - the meridional transport per unit width depends only on the local windstress.
Mathematical Description
Derivation
The development of Sverdrup's theory of the wind driven ocean circulation consists of two parts:
- Step 1 derivation of a simplified vorticity balance for the interior ocean
- Step 2 a vertical integration of step 1 under appropriate conditions, which yields a remarkable relationship between the vertically integrated meridional flow and the local value of the wind stress. Since we are now concerned with the ocean mixed layer, we can not neglect the internal stress terms.
Horizontal equations of motion
\begin{equation*} \frac{du}{dt} - fv = - \frac{1}{\rho} \frac{\partial P}{\partial x} + A_H \nabla^2_H u + \frac{1}{\rho} \frac{\partial \tau^x}{\partial z} \end{equation*}
\begin{equation*} \frac{dv}{dt} + fu = - \frac{1}{\rho} \frac{\partial P}{\partial y} + A_H \nabla^2_H v + \frac{1}{\rho} \frac{\partial \tau^y}{\partial z} \end{equation*}
- $A_H$ - horizontal eddy viscosity
- $\tau$ - horizontal stress acting on the ocean
- $\frac{\partial \tau}{\partial z} = \Bigl(\frac{\partial \tau^x}{\partial z} , \frac{\partial \tau^y}{\partial z}\Bigr)$ - is the vertical flux of horizontal momentum due to windstress forcing
Now we are interested in the entire water column, so we will redefine the ocean interior as the part of the ocean circulation away from the western boundary and equator, but includes the surface.
The equations of motion for the steady ocean circulation become
\begin{equation*} -fv = - \frac{1}{\rho} \frac{\partial P}{\partial x} + \frac{1}{\rho} \frac{\partial \tau^x}{\partial z} \end{equation*}
\begin{equation*} +fu = -\frac{1}{\rho} \frac{\partial P}{\partial y} + \frac{1}{\rho}\frac{\partial \tau^y}{\partial z} \end{equation*}
We will now consider the water column of the interior ocean as composed of two parts: s surface mixed layer of death $h_m$ above a deep abyss of depth $D$. In the mixed layer, due to the stirring action of wind, we know that $\partial \tau/\partial z$ will be important, so we have,
\begin{equation*} \rho f v = +\frac{\partial P}{\partial x} - \frac{\partial \tau^x}{\partial z} \end{equation*}
\begin{equation*} \rho f u = -\frac{\partial P}{\partial y} + \frac{\partial \tau^y}{\partial z} \end{equation*}
We now examine the vorticity balance of the region. First eliminate the $P$ terms
\begin{equation*} \frac{\partial(\rho fu)}{\partial x} + \frac{\partial(\rho fv)}{\partial y} = \frac{\partial (\frac{\partial \tau^y}{\partial x} - \frac{\partial \tau^x}{\partial y})}{\partial z} \end{equation*}
Applying the Boussinesque approximation, we can use $\rho_0$ to replace $\rho$ in the equation; converting and re-arranging yields to
\begin{equation*} \rho_0 \beta v = \rho_0 f \frac{\partial w}{\partial z} + \frac{\partial(\frac{\partial \tau^y}{\partial x} - \frac{\partial \tau^x}{\partial y})}{\partial z} \end{equation*}
Each term in the equation above, from left to right, is: advection of planetary vorticity, stretching term of water column, and vorticity input from windstress. Below the mixed layer the stress term can be ignored and we have the Sverdrup relation
\begin{equation*} \beta v = f \frac{\partial w}{\partial z} \end{equation*}
Now let's have a look at step 2, the vertical integration of vorticity equation over the entire water column, we have the Sverdrup Balance:
\begin{equation*} \beta V_s = \frac{curl \cdot \tau_w}{\rho_0} \end{equation*}
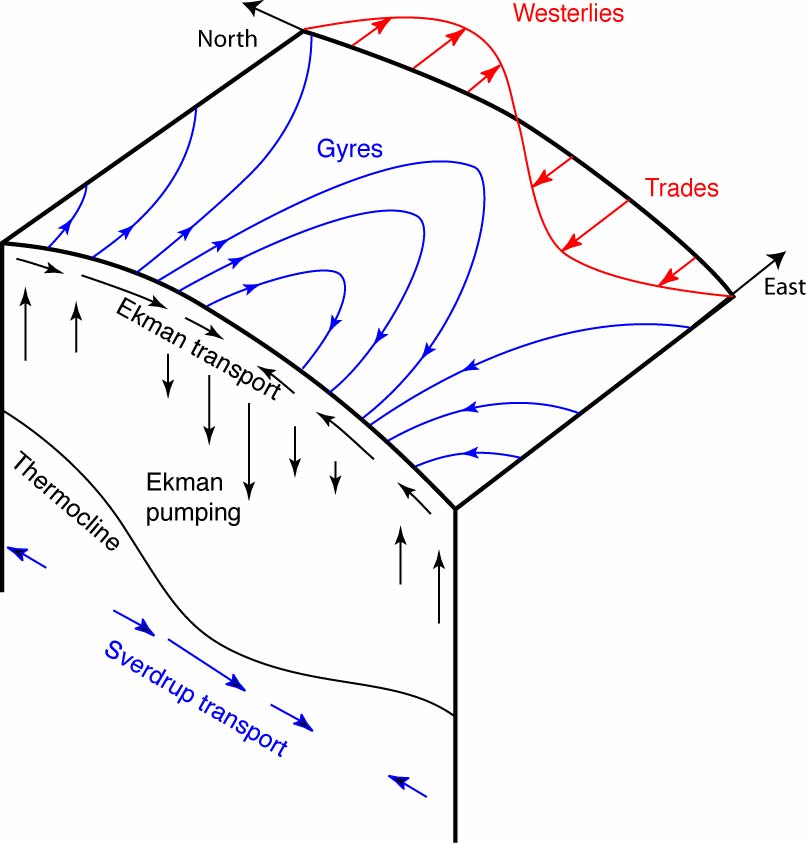
Application to ocean circulation: Sverdrup transport and gyre circulation
In the subtropical gyres, the interior flow is toward the equator in both the Northern and Southern hemispheres. In the subpolar gyres, the interior flow is poleward in both hemispheres. These interior flow is directions can be understood through the Sverdrup balance.
Consider a schematic of the subtropical North Pacific. The winds at the sea surface are not spatially uniform. South about 30°N, the Pacific is dominated by easterly trade winds. North of this, it is dominated by the westerlies. This causes northward Ekman transport under the trade winds, and southward Ekman transport under the westerlies. As a result, there is Ekman convergence throughout the subtropical North Pacific.
The convergent surface layer water in the subtropics must go somewhere so there is downward vertical velocity at the base of the (50 m thick) Ekman depth. At some level between the surface and ocean bottom, there is likely no vertical velocity. Therefore there is net suqashing of the water columns in the subtropical region (also called Ekman pumping).
In the ocean interior, relative vorticity is small, so planetary vorticity must decrease, which results in the equatorward flow that characterizes the subtropical gyre.
The subpolar North Pacific lies north of the westerly wind maximum at 40°N. Ekman transport is therefore southward, with a maximum at about 40°N and weaker at higher latitudes. Therefore there must be upwelling throughout the wide latitude band of the subpolare gyre. This upwelling stretches the water columns, which then move poleward, creating the poleward flow of the subpolar gyre.
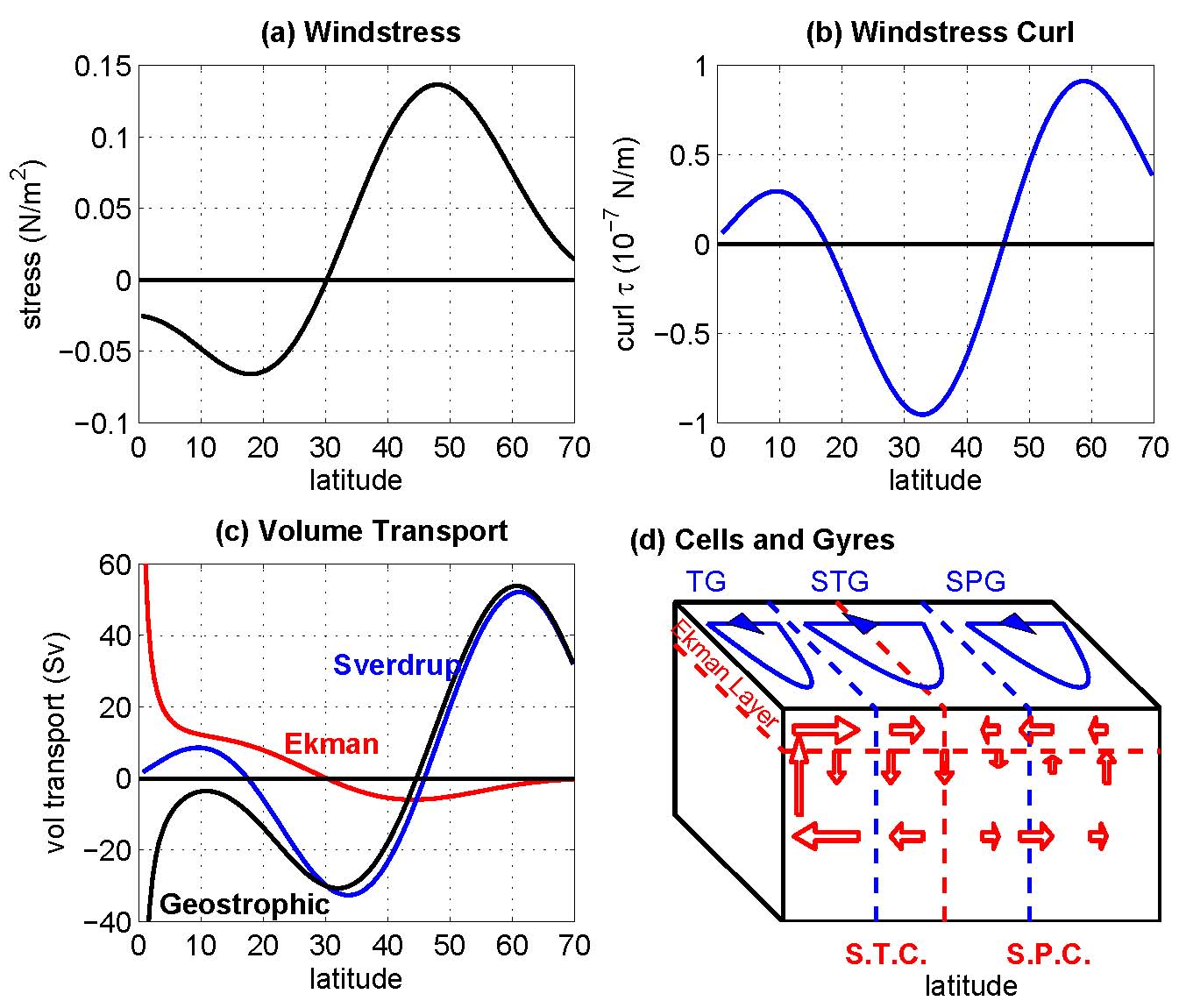
- a) idealized zonal wind stress as a function of latitute
- b) curl of wind profile shown in a)
- c) meridional volume transports given by Sverdrup relation, Ekman transport, and geostrophic component of the Sverdrup flow
- d) schematic showing barotropic gyres and Ekman/geostrophic cells (subtropical and subpolar)
References
- Talley, L. D. (2011). Descriptive Physical Oceanography - An Introduction.
- Klinger, B. A., Haine, T. W. N. (2011). Ocean Circulation in Three Dimensions. — webpage 2014/04/22 20:36
- Han W. (2013). Introduction to Physical Oceanography. — webpage 2014/04/22 20:41
Tasks FS2015
What are the units of $V_s$ and why?
Write the Sverdrup relation in $x$- and $y$-components.
Mention the resulting equation for $U_s$ resulting from incompressibility.