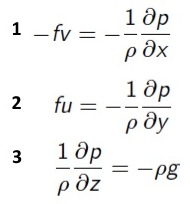Ocean Wiki

Author: Blanche Glück

In geostrophic currents the horizontal pressure gradient force is balanced by the Coriolis force. Instead of water is moving along the horizontal pressure gradient (from a region of high pressure to a region of low pressure) water moves at right angle to it parallel to the isobars. In the Northern Hemisphere, water flows with the high pressure to the right to it; in the Southern Hemisphere, water flows with the high pressure to the left to it (wikipedia, 2014).

This deflection is caused by the Coriolis force that comes from the Earth rotation.

Geostrophic currents occur in barotropic (homogenous) and baroclinic (with lateral variations in density) conditions (Brown et al., 2001).

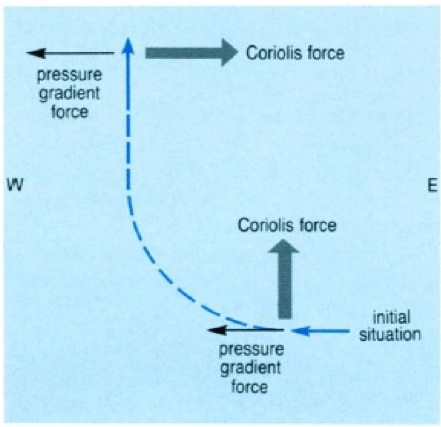
Figure 1: The Coriolis force acts on the water that moves from East to West along the pressure gradient (Brown et al., 2001)

Geostrophic equations are used to calculate currents at depth or to infer ocean currents from measurements of the sea surface height (by satellite altimeters) or from vertical profiles of seawater density taken by ships or autonomous buoys (wikipedia, 2014).

There is steady-state balance between pressure gradient force and Coriolis force. The equations for geostrophic balance are derived from the equations of motion.

Assumptions:

• steady state (no acceleration)
• hydrostatic balance
• no viscosity

Geostrophic equations (Münnich, 2014):

f = 2*Ω*sinφ (Coriolis parameter)

Geostrophic velocity (Münnich, 2014):

v = g/f *tanθ (v in modulus)

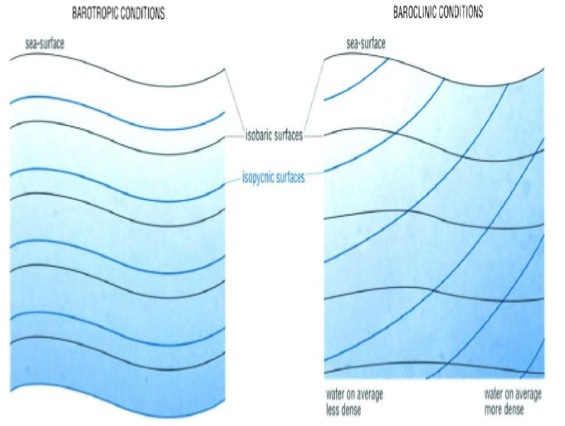
In barotropic conditions the isobaric surfaces follow the sea-surface, even at depth, and the isopycnic surfaces are parallel to it. So their slopes (between sea-surface and isobaric/isopycnic surface) stay constant with depth. Thus horizontal pressure gradient is constant with depth, so is the geostrophic current at right angles to it. In baroclinic conditions the extent to which isobaric surfaces follow the sea-surface decreases with increasing depth (the slope becomes smaller), as the density distribution has more and more effect. The horizontal pressure gradient decreases with depth, so does the geostrophic current (Brown et al., 2001).

Figure 2: Barotropic (ρ=ρ(p)) and barocline (ρ≠ρ(p)) conditions (Brown et al., 2001)

Level of no motion is a reference surface, at about 2000 m below the surface. It serves to convert the relative geostrophic velocities to velocities relative to the Earth. Currents are assumed to be zero at this depth, and relativ currents are integrated up to the surface and down to the bottom to obtain current velocity as a function of depth (oceanworld.tamu.edu, 2014).

(see lecture and tutorial 4)

References

• http://en.wikipedia.org/wiki/Geostrophic_current. Retrieved 30.04.2014
• http://oceanworld.tamu.edu/resources/ocng_textbook/chapter10/chapter10_06.htm. Retrieved 30.04.2014
• Brown,E.; Colling,A.; Park,D.; Phillips,J.; Rothery, D.; Wright, J. (2001), Ocean Circulation (Second Edition), Open University, Elsevier Ltd., pg.: 46-53
• Münnich, M., Lecture: Introduction to Physical Oceanography, wind-driven circulation I, 9 April 2014