Kelvin Waves
Author: Elisa Lovecchio
Kelvin waves are large-scale waves that propagate along boundaries.
They are generated by 3 factors: gravity, Earth rotation which causes a significant Coriolis acceleration and the presence of vertical boundaries as the edge of the continents or the Equator.
The fundamental difference between a Kelvin wave and a 2D gravity wave is that the latter can propagate in two directions on a plane while a Kelvin wave can propagate only in one direction due the presence of an obstacle.
The Coriolis force and consequent Ekman transport causes a piling up of fluid against the lateral boundary, and produces an offshore pressure gradient normal to the boundary line. This gradient must be balanced by the Coriolis force itself and is associated with a decreasing surface elevation of the water in the offshore direction.
Different kinds of Kelvin Waves
Kelvin waves can be divided into 2 groups according to the type of vertical boundary along which they propagate (coastal or equatorial Kelvin waves), and in other 2 subgroups each according to the depth at which they develop (internal or external Kelvin waves), generating then 4 possible different types of Kelvin waves.
Coastal Kelvin Waves
Consider a shallow layer of fluid with an upper free surface in a rotating system in presence of gravity.
Suppose that a lateral vertical boundary constrains the flow of the fluid, impeding to the particles of fluid to cross it, and obliging them to move only vertically or along its direction in its proximity.
Due to rotation and to the presence of the vertical obstacle, a certain amount of fluid will pile up in the region close to the obstacle and flow along its direction. The reaction of the wall will neutralize the effect of the Coriolis force, creating a pressure gradient normal to its direction, with an associated higher surface elevation of the water at the boundary.
This is the mechanism through which coastal Kelvin waves are formed.
If we observe the wave motion in proximity of the boundary or coastline, for any vertical section of the wave the motion will appear exactly the same of a gravity wave in absence of rotation.
Coastal Kelvin waves get shallower when moving along a boundary towards the north, since the amplitude of their oscillations decreases exponentially with the Coriolis parameter $\textcolor{black}{f}$.
Equatorial Kelvin Waves
Equatorial Kelvin waves propagate on the Equator (which acts as a wave-guide) in the eastward direction and develop as a consequence of the change of sign of the Coriolis parameter when passing from one hemisphere to the other.
This change of sign allows the Equator to act as a boundary for the wave propagation: the eastward flow of fluid along its direction induces a piling up of water on the Equator itself due to the induced equatorward Ekman transport in both hemispheres, and generates a meridional pressure gradient that impedes the water to cross the boundary. The profile of equatorial Kelvin waves on a section normal to the Equator line is Gaussian.
External Kelvin Waves
A Kelvin wave is called external when it occurs in barotropic conditions an penetrates the entire depth of the fluid. It is visible at the surface as a tilt in the sea surface height.
External Kelvin waves are non-dispersive (since they have the same characteristics of gravity waves due to the effect of the reaction of the boundary compensating the Coriolis force), and will propagate rigidly with the same wave speed $\textcolor{black}{c_e=\sqrt{gH}}$ of a gravitational wave in a layer of thickness $\textcolor{black}{H}$.
The amplitude of the wave will decrease exponentially with distance from the boundary, with a characteristic length called Rossby Radius of deformation defined as $\textcolor{black}{R_d = \dfrac{c}{f}}$ where $\textcolor{black}{c}$ is the wave speed and $\textcolor{black}{f}$ is the Coriolis parameter.
jSWmhkcPsHw
Internal Kelvin Waves
Internal Kelvin waves propagate between layers of water of very different density, and appear generally in conditions of higly stratified ocean. As for the external Kelvin waves, also internal Kelvin waves mantein the same characteristic of their non-rotational counterpart: internal gravity waves.
For a stratified fluid with two distinct overlapping layers of depths $\textcolor{black}{H_1}$ and $\textcolor{black}{H_2}$ and densities $\textcolor{black}{\rho_1}$ and $\textcolor{black}{\rho_2}$, the velocity of the internal Kelvin wave is then given by $\textcolor{black}{c_i=\sqrt{g'H'}}$ where we have defined $\textcolor{black}{H'=\dfrac{H_1 H_2}{H_1+H_2}}$ and the reduced gravity $\textcolor{black}{g'=g \dfrac{\rho_2-\rho_1}{\rho_2} \ll g}$.
Shallow water model: a bit of math!
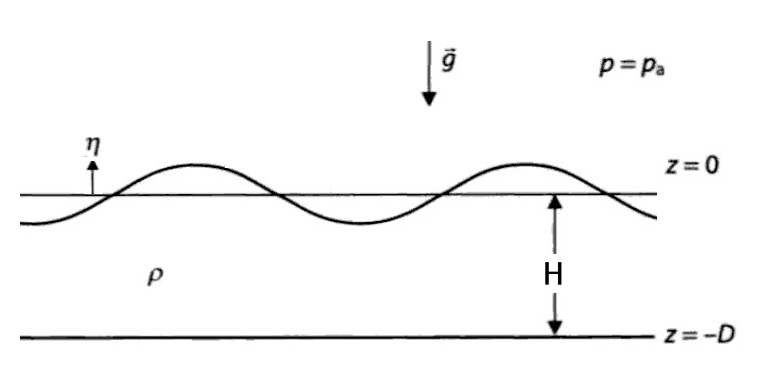Let's suppose to have a layer of liquid (water) in a gravitational field $\textcolor{black}{\vec g = (0, 0, -g)}$ on a rotating planet, with the rotation represented by the Coriolis parameter $\textcolor{black}{f}$.
Let's also suppose that the liquid has an upper free surface, which oscillates around the mean water elevation $\textcolor{black}{H}$. These small oscillations are represented by a 2D horizontal field $\textcolor{black}{\eta(x,y)}$.
We want to describe the oscillations $\textcolor{black}{\eta(x,y)}$ of the upper free-surface.
The system of equation that describes the motion of the fluid is:
\begin{equation*}
\textcolor{black}{
\begin{cases}
\dfrac{\partial u}{\partial t} - f v = - \dfrac{1}{\rho} \dfrac{\partial p}{\partial x} \qquad \qquad &\text{(1) $\rightarrow$ x-impuls}\\[.6em]
\dfrac{\partial v}{\partial t} + f u = - \dfrac{1}{\rho} \dfrac{\partial p}{\partial y} \qquad \qquad &\text{(2) $\rightarrow$ y-impuls}\\[.6em]
\dfrac{\partial w}{\partial t} = - \dfrac{1}{\rho} \dfrac{\partial p}{\partial z} - g \qquad \qquad &\text{(3) $\rightarrow$ z-impuls}\\[.6em]
\dfrac{\partial u}{\partial x} + \dfrac{\partial v}{\partial y} + \dfrac{\partial w}{\partial z} = 0 \qquad \qquad &\text{(4) $\rightarrow$ continuity equation: mass conservation}\\[.6em]
\end{cases}
}
\end{equation*}
with boundary condition $\textcolor{black}{w(z=-D)=0}$ since the water must have zero vertical velocity at the floor level.
We can simplify this system of equations through the so called shallow water approximation.
This approzimation assumes that the depth $\textcolor{black}{H}$ of the water column is much smaller than the lateral extension $\textcolor{black}{L}$ of the liquid layer, so that $\textcolor{black}{L>>H}$, and hence also vertical velocities must be very small compared to the horizontal components.
We have then $\textcolor{black}{w' \sim 0 \rightarrow \frac{\partial w'}{\partial t} \sim 0}$, which implies from equation (3) that pressure has a hydrostatic profile, in other words:
\begin{equation*}
\textcolor{black}{
\frac{\partial p}{\partial z} = - \rho g \qquad \Rightarrow \qquad p = \rho g (\eta(x,y) - z) + p_{atm}
\end{equation*}
where the last equation is an integrated form of the hydrostatic equation with $\textcolor{black}{p_{atm}(x,y,t)}$ being the atmospheric pressure field on the water surface, that we consider here constant $\textcolor{black}{p_{atm}(x,y,t)\sim p_{atm}}$.
Deriving this equation in the two horizontal directions we obtain:
\begin{equation*}
\textcolor{black}{
\frac{\partial p}{\partial x} = \rho g \frac{\partial \eta}{\partial x} \qquad \text{and} \qquad \frac{\partial p}{\partial y} = \rho g \frac{\partial \eta}{\partial y}
\end{equation*}
From the continuity equation (4) we obtain instead by vertical integration:
\begin{equation*}
\textcolor{black}{
\int_{-D}^{h=H+\eta} \bigg(\dfrac{\partial u}{\partial x} + \dfrac{\partial v}{\partial y} + \dfrac{\partial w}{\partial z}\bigg) dz = (H+\eta) \bigg( \dfrac{\partial u}{\partial x} + \dfrac{\partial v}{\partial y} \bigg) + \big(w(h)-w(-D)\big) \qquad \Rightarrow \qquad (H+\eta) \bigg( \dfrac{\partial u}{\partial x} + \dfrac{\partial v}{\partial y} \bigg) + \frac{\partial \eta}{\partial t} = 0
\end{equation*}
where we have used the boundary condition.
Our system of equations for a shallow layer of water in a rotating gravitational system becomes then:
\begin{equation*}
\boxed{
\textcolor{black}{
\begin{cases}
\dfrac{\partial u}{\partial t} - f v = - g \dfrac{\partial \eta}{\partial x}\\[.6em]
\dfrac{\partial v}{\partial t} + f u = - g \dfrac{\partial \eta}{\partial y}\\[.6em]
\dfrac{\partial \eta}{\partial t} + (H+\eta) \bigg( \dfrac{\partial u}{\partial x} + \dfrac{\partial v}{\partial y} \bigg) = 0\\[.6em]
\end{cases}
}
}
\end{equation*}
Shallow gravity waves
If we neglect the effect of rotation $\textcolor{black}{(f=0)}$ we can derive again the equations in the previous system (respectively in x, y and t) and combine them in one equation for the motion of the free surface.
\begin{equation*}
\textcolor{black}{
\begin{cases}
\dfrac{\partial u}{\partial t} = - g \dfrac{\partial \eta}{\partial x}\\[.6em]
\dfrac{\partial v}{\partial t} = - g \dfrac{\partial \eta}{\partial y}\\[.6em]
\dfrac{\partial \eta}{\partial t} + (H+\eta) \bigg( \dfrac{\partial u}{\partial x} + \dfrac{\partial v}{\partial y} \bigg) = 0\\[.6em]
\end{cases}
\qquad \Rightarrow \qquad
\begin{cases}
\dfrac{\partial}{\partial t} \bigg( \dfrac{\partial u}{\partial x} \bigg)= - g \dfrac{\partial^2 \eta}{\partial x^2}\\[.6em]
\dfrac{\partial}{\partial t} \bigg(\dfrac{\partial v}{\partial y} \bigg)= - g \dfrac{\partial^2 \eta}{\partial y^2}\\[.6em]
\dfrac{\partial^2 \eta}{\partial t^2} + (H+\eta) \dfrac{\partial}{\partial t}\bigg( \dfrac{\partial u}{\partial x} + \dfrac{\partial v}{\partial y} \bigg) = 0\\[.6em]
\end{cases}
\qquad \Rightarrow \qquad
\dfrac{\partial^2 \eta}{\partial t^2} - g (H+\eta) \bigg( \frac{\partial^2 \eta}{\partial x^2} + \frac{\partial^2 \eta}{\partial y^2} \bigg) = 0
}
\end{equation*}
obtained substituting the derivatives of the velocities in the last equation.
If we neglect all the terms that are quadratic in $\textcolor{black}{\eta}$, since $\textcolor{black}{\eta}$ is assumed to be very small, we obtain the shallow water gravity wave equation:
\begin{equation*}
\textcolor{black}{
\boxed{
\dfrac{\partial^2 \eta}{\partial t^2} = g H \bigg( \frac{\partial^2 \eta}{\partial x^2} + \frac{\partial^2 \eta}{\partial y^2} \bigg)
}
}
\end{equation*}
These 2-dimensional waves:
1) are non-dispersive, since phase and group velocity correspond to each other $\textcolor{black}{c_{ph} = c_g}$, and both are equal to $\textcolor{black}{c = \sqrt{g H}}$
2) respect the superposition principle, so that given two different solutions of the equation $\textcolor{black}{\eta_1(x,y,t)}$ and $\textcolor{black}{\eta_2(x,y,t)}$, their linear composition $\textcolor{black}{\eta(x,y,t) = \alpha \eta_1(x,y,t) + \beta \eta_2(x,y,t)}$ is still a solution of the wave equation.
This equation has sinusoidal solutions that propagate rigidly in space and time due to their non-dispersive nature. In the x direction we have for example:
\begin{equation*}
\textcolor{black}{
\eta(x,t) = f(x \pm ct) = A \cdot sin[k(x \pm ct)] = A \cdot sin(kx \pm \omega t)
}
\end{equation*}
where $\textcolor{black}{A}$ is the wave amplitude, and $\textcolor{black}{\omega = ck = 2 \pi/T}$ is called angular frequency.
External Kelvin Waves
If we go back to the shallow water system of equations and we do not neglect the Coriolis force but impose that the wave can propagate only in one direction (effect of the boundary), we can find Kelvin wave solutions.
To do so, we have to impose the boundary condition: suppose to have a vertical barrier along the x direction at $\textcolor{black}{y=0}$:
the component of the velocity vector normal to the barrier must vanish ($\textcolor{black}{v \equiv 0}$) in every point.
The shallow water system reduces then to:
\begin{equation*}
\textcolor{black}{
\begin{cases}
\dfrac{\partial u}{\partial t} = - g \dfrac{\partial \eta}{\partial x}\\[.6em]
f u = - g \dfrac{\partial \eta}{\partial y}\\[.6em]
\dfrac{\partial \eta}{\partial t} + H \dfrac{\partial u}{\partial x} = 0\\[.6em]
\end{cases}
}
\end{equation*}
From the second equation we can notice that the assumption on $\textcolor{black}{v}$ makes the flow geostrophic in the x direction.
If we combine the first and last equations, we find again an equation that is analogous to the gravity wave equation, but which allows only a 1-dimensional propagation along the x direction:
\begin{equation*}
\textcolor{black}{
\dfrac{\partial^2 \eta}{\partial t^2} = g H \bigg( \frac{\partial^2 \eta}{\partial x^2} \bigg)
}
\end{equation*}
As stated before the velocity of propagation along the boundary is the same of that of a shallow water gravity wave: $\textcolor{black}{c = \sqrt{g H}}$.
To find a solution for the 2-dimensional field of the surface height $\textcolor{black}{\eta(x,y)}$ we can instead seek for solutions for $\textcolor{black}{\eta(x,y)}$ and $\textcolor{black}{u(x,y)}$ of the form:
\begin{equation*}
\textcolor{black}{
\begin{align}
\eta(x,y)= \eta_0(y) \cdot e^{i(k x-\omega t)}\\
u(x,y)= u_0(y) \cdot e^{i(k x-\omega t)}
\end{align}
}
\end{equation*}
where we suppose to have an amplitude of the wave oscillation that changes with the distance from the boundary, that is in the y direction.
Sobsituting this solutions in the previous system, we find
\begin{equation*}
\textcolor{black}{
\begin{cases}
-\omega u_0(y) = - g k \eta_0(y)\\[.6em]
f u_0(y) = - g \dfrac{\partial \eta_0(y)}{\partial y}\\[.6em]
- \omega \eta_0(y) + H k u_0(y) = 0\\[.6em]
\end{cases}
}
\end{equation*}
in the unknowns $\textcolor{black}{\eta_0(y)}$, $\textcolor{black}{u_0(y)}$, $\textcolor{black}{\omega}$ and $\textcolor{black}{k}$.
This system gives us two important pieces of information:
1) getting rid of $\textcolor{black}{\eta_0(y)}$ and $\textcolor{black}{u_0(y)}$ we find the dispersion relation $\textcolor{black}{\omega(k)= \sqrt{g H} \cdot k = c k}$ that confirms the fact that Kelvin waves are non-dispersive since phase and group velocity have the same value $\textcolor{black}{c = \sqrt{g H}}$, that is again the one we have found for gravity waves.
2) combining the first two equations we find a differential equation for the amplitude $\textcolor{black}{\eta_0(y)}$ of the small oscillations, that we can solve:
\begin{equation*}
\textcolor{black}{
\dfrac{\partial \eta_0(y)}{\partial y} = -\frac{f}{g} \cdot u_0 = -\frac{f}{g} \bigg(g \frac{k}{w} \eta_0(y) \bigg) = - \frac{f}{c} \cdot \eta_0 (y) \qquad \Rightarrow \qquad \int \dfrac{d \eta_0(y)}{\eta_0(y)} = - \int \frac{f}{c} dy \qquad \Rightarrow \qquad \eta_0(y) = \eta_0 \cdot e^{-\frac{f}{c}y}
}
\end{equation*}
The general real solution for the oscillations of a Kelvin with a boundary along the x-direction at $\textcolor{black}{y=0}$ wave is then:
\begin{equation*}
\textcolor{black}{
\boxed{
\eta_0(x,y,t) = \eta_0 \cdot e^{-\frac{y}{R_d}} \cdot \cos(k x-\omega t) \\[.6em]
}
}
\end{equation*}
where we have defined the Rossby radius of deformation $\textcolor{black}{R_d = \dfrac{c}{f}}$, which is the characteristic length for the offshore exponential decay of the amplitude of the Kelvin wave oscillation.
Internal Kelvin Wave
Maybe in the future also this section will appear :)
Kelvin Waves and ENSO
Kelvin waves are particularly important for the transport of information on a planetary scale.
In particular regarding ENSO, Kelvin waves are responsible for the propagation of disturbances in the water temperature at depth: in the months preceding an El Nino event, warm anomalies are generally observed in a depth range between 100m and 200m; these anomalies propagate along the Equator as internal Kelvin waves, moving from west to east and finally reaching the South American coast, where they emerge and give rise to the warm pool anomaly.
References
B. Wang University of Hawaii, “Kelvin Waves”, Elsevier Science (2002)
Anna von der Heydt, “Rossby and Kelvin waves”, Utrecht summer school Physics of the climate system (August 19-30, 2013)
Comments
Shorten the article and add a section on internal Kelvin Waves.
