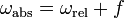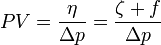Table of Contents
Vorticity
Author: Ronny Meier
The vorticity (ω) of a velocity field is used in fluid dynamics to describe the local spinning of the fluid. In other words it expresses how a fluid particle moves relatively to the particles in the fluid just next to it. To understand the effects of the vorticity better it is useful to imagine one part of the fluid to become solid. Would the particle rotate around its own axis while moving with the flow this would mean that the velocity field has a vorticity unequal to zero.
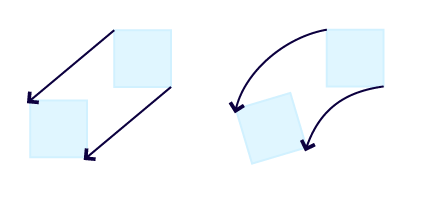
ω=0 ω≠0
Mathematically the vorticity is defined with the following formula:
Often in Meteorology and Oceanography only the z-component of this vector field is used since the x- and the y-component are rather small in praxis:
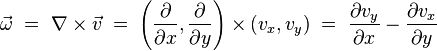
With v being the velocity component in y-direction and u in x-direction. Note that this simplified vorticity is actually still a vector pointing in z-direction.
Absolute and relative vorticity
While the absolute vorticity describes the vorticity of the flow related to an inertial reference frame the relative vorticity refers to the reference frame earth which is rotating itself. The absolute vorticity is the sum of the relative vorticity and the earths rotation:
Potential vorticity
The potential vorticity (generally q) is defined as the absolute vorticity (here η) divided by the height of the whole rotating water (or air) column (Δp here).
It can be shown (see lecture notes) that the potential vorticity (PV) is conserved for a frictionless rotation. This law can be used to determine the change of the relative vorticity of water columns which move north- or southwards (f changes) or to regions with different depth (H changes). The PV can also be expressed with the help of the density of the fluid and its potential temperature:
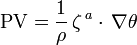
Sources
http://en.wikipedia.org/wiki/Vorticity May 2014
http://en.wikipedia.org/wiki/Potential_vorticity May 2014