Table of Contents
Stommel Theory of the Gulf Stream
Author: Seraina Klaus
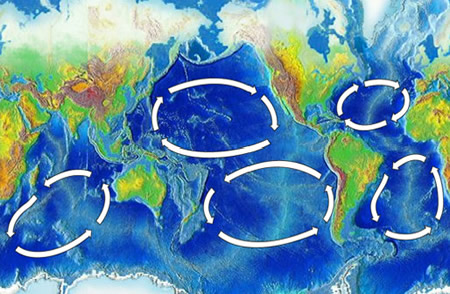
Western Boundary Current
Surface currents located on the western side of the subtropical gyres, so-called western boundary currents, are faster than their eastern counterparts. In fact, they are among the fastest surface currents in the ocean. One reason for the westward intensification of boundary currents has to do with the strengthening of the Coriolis effect with latitude. The Coriolis effect is stronger in the latitudes of the westerlies than in the latitudes of the trade winds. Transport of surface waters toward the western boundary of the ocean basins causes the ocean-surface slope to be steeper on the western side (versus eastern side) of a gyre (in either hemisphere). A steeper ocean-surface slope translates into a faster geostrophic flow on that side of the gyre.
Waters in western boundary currents typically move 40 to 120 km per day. These currents also extend much deeper than most other surface currents, down to a depth of 1000 m or more. Thus, the strong western boundary currents are so deep that they are deflected by the continental margins, which prevent these currents from flowing onto the shallow continental shelves. Eastern boundary currents, such as the California Current and the Canary Current, are slower, shallower, and wider than the western boundary currents. Similar to the return flow in a household heating system, these currents transport colder waters into the tropics where they are heated and transported poleward in the western boundary currents.
Waters moving in the western boundary currents adjacent to the major gyres (North and South Pacific and Atlantic basins and the Indian basin) transport large quantities of heat poleward from the tropics. Among these boundary currents are the Gulf Stream and the Kuroshio (off Japan) (Movie 1), which rank next in volume of water flow to the Antarctic Circumpolar Current. The Southern Hemisphere's western boundary currents include the Agulhas Current (off southeast Africa), the Brazil Current, and the East Australia Current. These currents are weaker than those in the northern ocean basins, in part because western boundary currents require extended land barriers that are generally absent in the Southern Hemisphere. Flows in the major western boundary currents are 50 to 100 times the total water discharged by all the world's rivers.
Example: The Gulf Stream Current
The Gulf Stream is a powerful western boundary current in the North Atlantic. Originating in the Gulf of Mexico, waters in the Gulf Stream travel at speeds of about one to three knots (1.85-5.55 kilometers per hour). The Gulf Stream influences the climate of the east coast of Florida, keeping temperatures warmer in the winter and cooler than the other southeastern states in the summer. Since it also extends toward Europe, it warms western European countries as well. (Figure 2)
More western boundary currents:
- North Atlantic – Gulf Stream
- North Pacific – Kuroshio
- South Atlantic – Brazil Current
- South Pacific – East Australian Current
- South Indian – Agulhas Current
Stommel's Theory of Western Boundary Currents
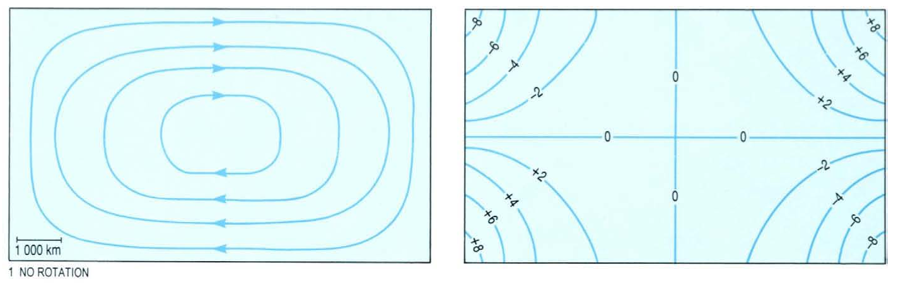
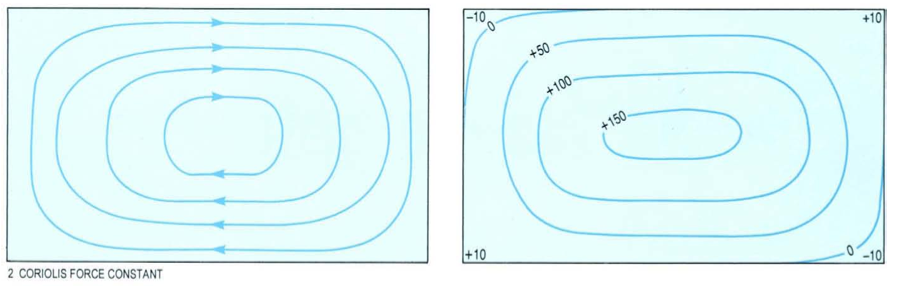
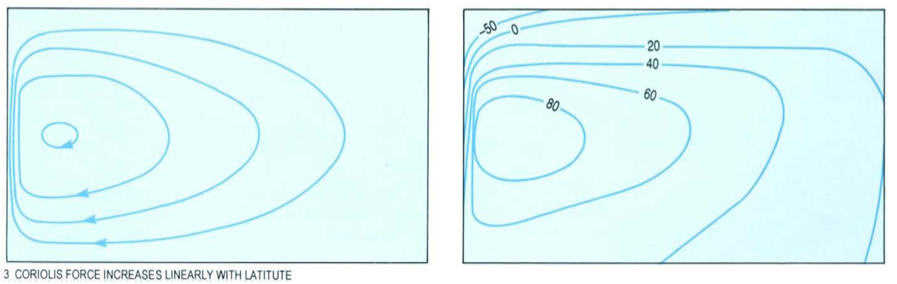
Sverdrup's theory was an advance on Ekman's in that the ocean was not assumed to be unlimited. However, it could not take account of a western boundary, and certainly could not explain the existence of intense western boundary currents like the Gulf Stream. This problem was solved by the American oceanographer Henry Stommel (1948). Stommel considered the effect of a symmetrical anticyclonic wind field on a rectangular ocean in three different situations:
1. The ocean is assumed to be on a non-rotating Earth. (Figure 3)
2. The ocean is rotating but the Coriolis parameter f is constant. (Figure 4)
3. The ocean is rotating and the Coriolis parameter varies with latitude. For the sake of simplicity, this variation is assumed to be linear. (Figure 5)
Stommel included friction in his calculations and he worked out the flows that would result when the wind stress and frictional forces balanced for each of the three situations described above.
Fig. 3-5: Summary of the results of Stommel's calculations.
This is how Stommel showed that intensification of western boundary currents is, in some way, the result of the fact that the Coriolis parameter varies with latitude, increasing from the Equator to the poles. Stommel also explained intensification of western boundary currents in terms of vorticity balance.
Vorticity concept in Stommel Theory
Imagine a subtropical gyre in the Northern Hemisphere, acted upon by a symmetrical wind field. If the wind has been blowing for a long time, the ocean will have reached a state of equilibrium, tending to rotate neither faster nor slower with time at every point in the ocean. The relative vorticity has a fixed value. This means that, over the ocean as a whole, those factors which act to chance the relative vorticity of the moving water must cancel each other out. Assuming for convenience that the depth of the flow is constant, we will now consider in turn each of the factors that affect relative vorticity.
The most obvious factor affecting the relative vorticity of the water in a gyre is the wind. The wind field is symmetrical and acts to supply negative (clockwise!) vorticity over the whole region.
The next factor to consider is change in latitude. Water moving northwards on the western side of the gyre is moving into regions of larger positive planetary vorticity and hence acquires negative relative vorticity. Similar: Water moving southwards on the eastern side of gyre is moving into regions of smaller positive planetary vorticity and so loses negative relative vorticity. However, because as much water moves northwards as moves southwards, the net change in relative vorticity of water in the gyre as a result of change in latitude is zero.
More explanations about vorticity you will find here.
What is the difference between the Stommel and Sverdrup Theories?
In 1947, the Scandinavian oceanographer Harald Sverdrup used mathematics to demonstrate another surprising relationship between wind stress and ocean circulation. Sverdrup's aim was to determine current flow in response to wind stress and horizontal pressur gradients. Unlike Ekman, Sverdrup was not interested in determining how horizontal flow varied with depth; instead, he derived an equation for the total or net flow resulting from wind stress. There are two types of current flow resulting from wind stress:
1. Ekman transport at right angles to the direction of the wind.
2. Geostrophic flow, in response to horizontal pressure gradients caused by the piling up of water through Ekman transport.
Sverdrup combined these components mathematically and obtained the flow pattern. The 'gyre' is not complete because deducing this flow pattern, Sverdrup considered the effect of an eastern boundary but could not also include the effect of a western boundary. As a result, there could be no northward flow in a 'Gulf Stream'.
The most interesting aspect of Sverdrup's result, however, was that the net amount of water transported by a given pattern of wind stress depends not on the absolute value of the wind stress but on its torque (i.e. its tendency to cause rotation).
In summary then, Sverdrup showed that at any location in the ocean, the total amount of water transported meridionally in the wind-influenced layer is proportional to the torque of the wind stress. Sverdrup's theory was an advance on Ekman's in thatthe ocean was not assumed tobe unlimited. However, it could not take account of a western boundary, and vertainly could not explan the existence of intense western boundary currents like the Gulf Stream. This problem was solve by Henry Stommel, as explained above.
References
- Introduction to Physical Oceanography. Lesson 14.4.2014.
- Ocean Circulation, Open University; Chapter 4.1. - 4.2.3., The North Atlantic Gyre: Observations and Theories
- http://oceanmotion.org/html/background/western-boundary-currents.htm, Retrieved: 3.5.2014
- http://oceanworld.tamu.edu/resources/ocng_textbook/chapter11/chapter11_02.htm, Retrieved: 3.5.2014