Table of Contents
The Principle of Mass Conservation and Transport Equations
Author: Rebecca Ritter
Amendments by Mirjam Miller
Primary Tools for Understanding Transport Equations
In order to be able to grasp the concepts of the primitive equations, which were introduced in the lecture, certain tools need to be introduced.
The Continuum Hypothesis
The continuum hypothesis is an integral part of physics, especially in the field of fluid dynamics. The basics of it rely on the microscopic scale properties of solids, liquids, and gases.
- Solids such as a block of wood, when disturbed, are unlikely to budge due to their strong intra-molecular forces, the small molecular spacing, and their severely constrained relative molecular movement.
- Gas such as air, on the other hand, has weak intra-molecular forces, very large molecular spacing, and relatively unconstrained molecular movement.
- Liquid such as water, being the intermediate between the two, has average intra-molecular forces, intermediate relative molecular movement, and moderate molecular spacing.
What do the relationships between the different states of matter on a microscopic scale have to do with the continuum hypothesis? Well, solids will not budge once disturbed. Gas and liquid, however, will. This is because any type of disturbance, let us say through movement, will effect the balance of forces within that body or parcel, and these matters will continuously amend their shapes until a uniform distribution succeeds. In other words, distortion leads to a transfer of heat or momentum within the fluid, which concludes in continuous movement as you would see in a propagating wave.
To note, the continuum hypothesis is defined for macroscopic scales. A parcel of liquid will have the same properties (similar to those listed above) throughout itself. This parcel can be described as a flow system in a continuous field. The laws, which are usually used in context with the continuum hypothesis are the laws of thermodynamics, Newton's laws of motion, an equation of state (eos), and the principle of mass conservation.
The Material Derivative
The material derivative, also referred to as the total derivative, is a type of operator one could argue. The concept of this material derivative has to do with the way one looks at a change. A local derivative (see table below) depicts a change without movement. An example for a local derivative is the change in temperature during the day (while never changing location). Simplified, one could state, that the material derivative describes a change in parameter while changing settings. The corresponding example would be the temperature change in a day while changing location (as this would be the case on a sailing ship).
The material derivative operator is defined as
$\frac{D}{D{t}} := \frac{\partial}{\partial {t}} + u \frac{\partial}{\partial{x}} + v \frac{\partial}{\partial{y}} + w \frac{\partial}{\partial{z}} = \frac{\partial}{\partial{t}}+ \vec{u} \cdot \nabla $,
where $\vec{u}$ refers to the three dimensional velocity vector with the components u (for x-dimension), v (for y-dimension), and w (for z-dimension).
For more information on the material derivative and how to use it, watch this informative YouTube video: https://www.youtube.com/watch?v=1tyw1_YE6rA.
Fick's 1st Law
Fick's first law describes the diffusive flux (down-gradient flux) under the assumption of steady state. The flux always leads from regions of high concentration to regions of low concentration. To accurately describe the diffusion-controlled flux we need to insert a diffusion coefficient, which is proportional to the velocity of particles squared.
\begin{equation*} \vec{J} = -D {\nabla}C \end{equation*}
$\vec{J}$: Diffusive flux. Measures the amount of substance that will flow through a small area during a small time interval [mol/m²s]].
$ D$: Diffusion coefficient [m²/s]
$\nabla$: Nabla Operator a Gradient Operator for 2 or more dimensions 1)
The Principle of Mass Conservation
For understanding the principle of mass conservation, we need to try to imagine a parcel with lengths of ${\partial x}$, ${\partial y}$, and ${\partial z}$. The corresponding Volume would therefore be ${\partial x}{\partial y}{\partial z}$, and the mass would be $\rho {\partial x}{\partial y}{\partial z}$. With these preliminary settings we can describe the continuity equation through flow balance equations.
Flow Balance Equations
The parcel in question has a scalar variable A. This will be accumulated in the following way: 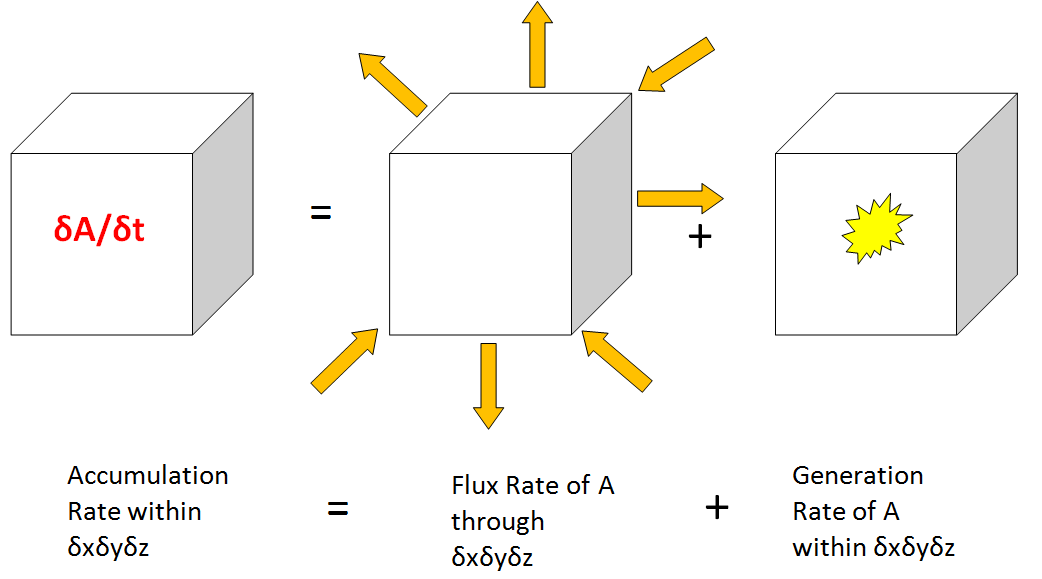
- The mathematical term for the accumulation rate is
\begin{equation*} \frac{\partial A}{\partial t} {\partial x}{\partial y}{\partial z} \end{equation*}
- The mathematical term for the flux rate of A into the volume is a bit more complicated. The flux's, or flow through an area's, approximation is derived for each component at a time, which will give us
\begin{equation*} -\left(\frac{\partial}{\partial x}(Au) + \frac{\partial}{\partial y}(Av) + \frac{\partial}{\partial z}(Aw)\right) {\partial x}{\partial y}{\partial z} \end{equation*}
- The mathematical term for the generation rate is similar to the flux rate, but will also account for changes in time. It is
\begin{equation*} \left(\frac{\partial A}{\partial t} + \frac{\partial}{\partial x}(Au) + \frac{\partial}{\partial y}(Av) + \frac{\partial}{\partial z}(Aw) \right) {\partial x}{\partial y}{\partial z} \end{equation*}
and for a randomly small parcel volume this will result in
\begin{equation*} \frac{\partial {A}}{\partial{t}} + \frac{\partial}{\partial x}(Au) + \frac{\partial}{\partial y}(Av) + \frac{\partial}{\partial z}(Aw) = S(A), \end{equation*}
where S(A) describes the net generation, which accounts for both sources and drains.
The Continuity Equation
By baring these three terms in mind, the continuity equation will seems more evident than without. First off, the scalar variable A will now be defined as $\rho$. The terms will now conclude with $\rho{\partial x}{\partial y}{\partial z}$ as the mass to the continuity equation:
\begin{equation*} \frac{\partial \rho}{\partial t} + \frac{\partial}{\partial x}(\rho u) + \frac{\partial}{\partial y}(\rho v) + \frac{\partial}{\partial z}(\rho w) = 0, \end{equation*}
which is the same as
\begin{equation*} \frac{D{\rho}}{D{t}} + \rho\cdot \left( \frac{\partial{u}}{\partial{x}} + \frac{\partial{v}}{\partial{y}} + \frac{\partial{w}}{\partial{z}} \right) = 0. \end{equation*}
In vector notation:
\begin{eqnarray*}
& & \frac{\partial{\rho}}{\partial{t}} + \nabla \cdot ( \rho \vec{u}) = 0 \\
& & \frac{\partial{\rho}}{\partial{t}} + \vec{u} \cdot \nabla \rho + \rho (\nabla \cdot \vec{u}) = 0 \\
& & \frac{D{\rho}}{D{t}} + \rho (\nabla \cdot \vec{u}) = 0.
\end{eqnarray*}
This relationship represents the principle of mass conservation, which is the same as the continuity equation.
If the fluid is incompressible (also called homogeneous fluid) the density of each fluid parcel remains constant 2), thus the continuity equation reduces to the diverging term which will then be zero (no divergence).
Incompressible fluid/homogeneous fluid: $\rho\;$ = const. \begin{equation*} \frac{D{\rho}}{D{t}} = 0 \Rightarrow \mathrm{div}\;\vec{u} = \nabla \cdot \vec{u} = 0 \end{equation*}
Term definitions
| Definition | Term |
|---|---|
| Material Derivative Operator | $ \frac{D}{Dt} := \frac{\partial}{\partial t} + u \frac{\partial}{\partial x} + v \frac{\partial}{\partial y} + w \frac{\partial}{\partial z} = \frac{\partial}{\partial t}+\vec{u} \cdot \nabla $ |
| Local Derivative | $ \frac{\partial }{\partial t}$ |
| Advection | $ \vec{u} \cdot \nabla\rho $ |
| Divergence | $ \nabla\cdot \vec{u}$ (a skalar!) |
Transport Equations for Tracer
The transport equation for tracers can be derived analogously to the continuity equation. Here, however, the scalar variable A describes the tracer's concentration, and will be written as $C_i$. Also here the net generation $S(A)$, or now in this particular case $S(C_i)$, will not be equal to zero:
\begin{equation*} S (C_i)= Q_i \neq\ 0 \end{equation*}
The tracer equation is
\begin{equation*} \frac{\partial C_i}{\partial t} + \frac{\partial}{\partial x}(C_i u) + \frac{\partial}{\partial y}(C_i v) + \frac{\partial}{\partial z}(C_i w) = Q_i \end{equation*}
which can also be written as
\begin{equation*} \frac{DC_i}{Dt} + C_i\cdot ( \frac{\partial u}{\partial x} + \frac{\partial{v}}{\partial{y}} + \frac{\partial{w}}{\partial{z}} ) = Q_i \end{equation*}
or
\begin{equation*} \frac{D{C_i}}{D{t}} +\vec{\nabla}(C_i\vec{u}) = Q_i. \end{equation*}
| Definition | Equation | Term definition | Term |
|---|---|---|---|
| Tracer Equation (no diffusion) | $ Q_i=\frac{\partial{C_i}}{\partial{t}} + \nabla \cdot (C_i \vec{u} ) $ | Change of parcel concentration Local Derivative Sink/Source | $ \frac{\partial{C_i}}{\partial{t}} $ $ Q_i $ |
| Tracer Equation with diffusion 3) | $Q_i -\nabla \cdot \vec{J_D} = \frac{\partial{C_i}}{\partial{t}} + \nabla \cdot (C_i \vec{u} ) $ | Diffusion | $ -\nabla \cdot \vec{J_D} $ |
| Tracer Equation for Seasalt S (for $ C_{i} = S$ and no salt sources $ Q_{S} = 0$) | $ \rho \frac{DS}{Dt} = \nabla \cdot (\rho{k_s} \nabla {S}) $ | Material Derivative of Salinity | $ \frac{DS}{Dt} $ |
Temperature Equation
The temperature equation presents different from the transport or continuity equation. It is different because when we look at the temperature, we would preferably do so with the potential temperature (temperatures).If we, however, refer to the adiabatic (isentropic) case our material derivative of this potential temperature will be zero:
\begin{equation*} \frac{D\theta}{Dt} = 0. \end{equation*}
Thus we receive the following temperature equation
\begin{equation*} \rho{c_p}\frac{DT}{Dt} - \alpha {T}\frac{Dp}{Dt} = 0, \end{equation*}
where $\rho$ refers to the density, $c_p$ to the specific heat capacity, and $\alpha$ to the coefficient of thermal expansion.
If we include temperature diffusion, Fick's Law needs to be used for all three dimensions4). This concludes to
\begin{equation*} \rho{c_p}\frac{DT}{Dt} - \alpha {T}\frac{Dp}{Dt} = \vec{\nabla} \cdot ({k_T}\vec{\nabla} {T}). \end{equation*}
To receive the final version of this equation it needs to account for sources and sinks, making $S(A)\neq 0$. Such sources and sinks could be an internal heat source $Q_T$ or an external heat flux $\vec{J_T}$, e.g., solar radiation.
\begin{equation*}
\rho{c_p}\frac{DT}{Dt} - \alpha {T}\frac{Dp}{Dt} = \vec{\nabla} \cdot ({k_T}\vec{\nabla} {T} +{J_T})+ {Q_T},
\end{equation*}
References
- Imboden, D., and Koch, S. (2003). Systemanalyse - Einführung in die mathematische Modellierung natürlicher Systeme. Springer-Verlag, Berlin Heidelberg.
- Marshall, J., and Plump, R. Alan (2007), Atmosphere, Ocean, and Climate Dynamics
- Muennich, M. (2015). Slides: Lecture 4. Lecture: Introduction to Physical Oceanography
- Wernli, H., and Pfahl, S. (2014), Script: Introduction to Environmental Fluid Dynamics
- Wernli, H., and Pfahl, S. (2014a), Script: Introduction to Environmental Fluid Dynamics
- Wernli, H., and Pfahl, S. (2014b), Slides: Chapter 3 - part B. Lecture: Einfuehrung in die Umwelt-Fluiddynamik.
Study Tasks
These three tasks could help you with your exam preparation:
- Determine the equations in $x,y,z$ coordinates.
- Determine the various transport equations, especially the one for salt.
- Try to explain the equation and its components in words.