Table of Contents

Equation of State

Author: Roland Häberli, Gabriela Schär

An equation of state is a relation between state variables. It is a thermodynamic equation which describes the state of matter under a given set of physical conditions, typically relating energy, temperature, volume, and pressure. Equations of state most commonly are used to describe the properties of fluids, such as liquids, gases, and plasma.

With this equation it's possible to calculate the density of pure water or seawater with dependency to temperature, salinity or pressure.

Equation of State for Pure Water

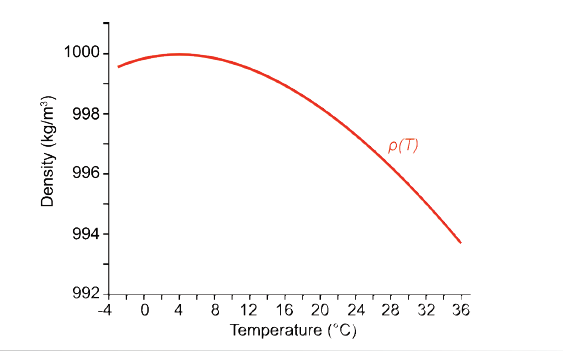
The following equation is used to calculate the density of fresh water. The polynomial structure results graphically in a parabola which shows the denisty anaomaly of pure water.

ρ(T) = 999.842594 + 6.793952 * 10-2T - 9.095290*10-3T2 + 1.001685*10-4T3 - 1.120083*10-6T4 + 6.536332*10-9T5

Parabolic function of density

Pure water shows a density anomaly. Maximum at 4°C, 1000 kgm-3 and p = 1013 hPa.

Thermal Bar

Definition:

A frontal interface characterised by a strong mixing of waters at and near the temperature of maximal density in large deep temperate lakes during spring warming. (Terzhevik 2012)

Thermal bar

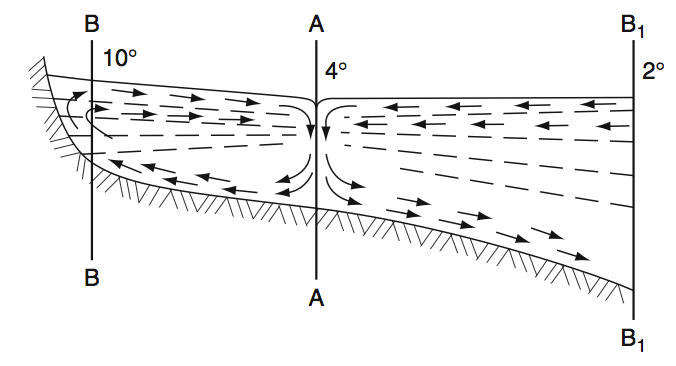
Fig: Scheme of the density-driven circulation in the near shore zone of a lake during the thermal bar existence. Lines BB, AA, B1B2 mark the near shore warm, thermal bar and cold zones, respectively. (Terzhevik 2012)

In spring typically water in lakes starts warming. The heat flux originates mainly from meteorological factors (solar radiation) and varies weakly in horizontal directions. So shallow near shore zones of a waterbody are heated up much faster as the rest of the lake. Because of the anomaly of the equation of state of fresh water, the stratification of density shows different behaviour in shallow and deep water zones. The shallow zones are hydrostatically stable and the deep water zones unstable. Between these zones the formation of double-cell convection with strong descending current between the cells are expected. This barrier inhibits mixing of water between the zones. Therefore dissolved substances including pollutants that come with the inflow (eg. rivers) are trapped in the warmer shore zones. As the warming proceeds, the thermal bar propagates offshore till the deep-water temperature reaches 4°C. This may take about one month. The same phenomena could theoretically occur in autumn due to preferential cooling of shallow zones. Autumnal thermal bars are likely much less because of smaller temperature gradients and strong wind induced dynamics. (Zilitinkevich et al 1992, Therzhevik 2012)

Equation of State for Seawater

TEOS-10

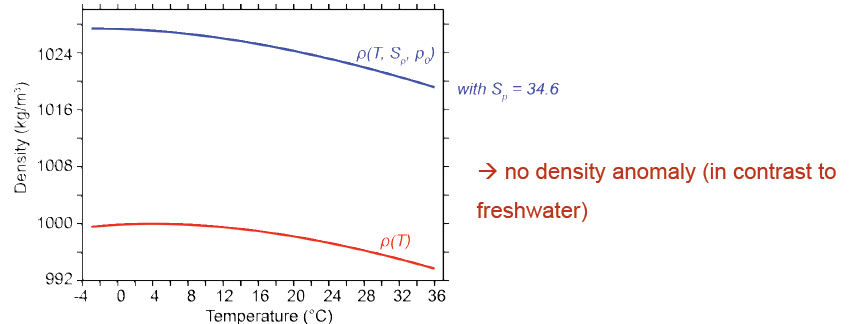
The Thermodynamic Equation Of State – 2010 (TEOS-10) is based on a Gibbs function formulation from which all thermodynamic properties of seawater (density, enthalpy, entropy sound speed, etc.) can be derived in a thermodynamically consistent manner. TEOS-10 was adopted by the Intergovernmental Oceanographic Commission at its 25th Assembly in June 2009 to replace EOS-80 as the official description of seawater and ice properties in marine science. In contrast to the EOS-80 the TEOS-10 uses the absolute salinity SA and the conservative temperature Θ instead of pratical salinity SP and potential temperature θ.

EOS-80

The formula EOS-80 from the year 1980 uses the practical salinity SP scale and the potential temperature θ to calculate the density.

ρ(S,T,p) = ρ(S,T,0) / [1-p/K(S,T,p)]

The EOS-80 is calculated in 3 steps:

Temperature dependency

ρ(T) = 999.842594 + 6.793952 * 10-2T - 9.095290*10-3T2 + 1.001685*10-4T3 - 1.120083*10-6T4 + 6.536332*10-9T5

Salinity dependency

ρ(T, SP, p0) = ρw + (0.824493 - 4.0899 * 10-3T + 7.6438 * 10-5T2 - 8.2467*10-7T3 + 5.3875 * 10-9T4)SP + (-5.72466 * 10-3 + 1.0227 * 10-4T - 1.6546 * 10-6T2)SP3/2 + 4.8314 * 10-4SP2

Pressure dependency

Kw value for pure water.

Kw = 19652.21 + 148.4206T - 2.327105T2 + 1.360477 * 10-2T3 - 5.155288 * 10-5T4

K value with salinity dependence and pressure p0.

K(T, SP, p0) = Kw + (54.6746 - 0.603459T + 1.09987 * 10-2T2 - 61670 * 10-5T3)SP + (7.944 * 10-2 + 1.6483 * 10-2T)SP3/2

Put all together and calculate the final K value.

K(T, SP, p) = K(T, SP, p0) + p(3.239908 + 1.43723 * 10-3T + 1.16092 * 10-4T2 -5.77905 * 10-7T3) + pSP(2.2838 * 10-3 - 1.0981 * 10-5T - 1.6078 * 10-6T2) + 1.91075 * 10-4 * pSP2/3 + p2(8.50935 * 10-5 - 6.12293 * 10-6T + 5.2787 * 10-8T2) + p2SP(-9.9348 * 10-7 + 2.0816 * 10-8T + 9.1697 * 10-10T2)

seawater vs. pure water

References

Comments