Table of Contents
Stratification & Buoyancy Frequency
Author: Simon Matter. Revised by: Emma Velterop.
Stratification
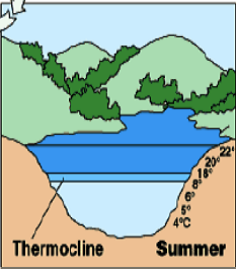
Looking at lakes in higher latitudes the water profile varies substantially between spring and summer; in spring the water temperature is equally distributed at around 4°C and the lake thus well mixed, whereas in summer the lake is stably stratified. This means that the colder water (closer to a temperature of 4°C) is denser and lies at the bottom of the lake, and the warmer and less dense the water becomes, the nearer it is to the surface.
This stratification in lakes also leads to the well-known effects of oxygen depletion in deep water, since diffusion is limited through the distinct strata. However, in the ocean, due to salinity the function for temperature becomes much more complex (state equation). The ocean is over all seasons mainly well stratified (except e.g. unstable situation in polar regions due to cabbeling (process in which two water parcels of the same density but differing temperatures and/or salinities mix and produce a water parcel of higher density, which subsequently sinks), which leads to deep water formation) and thus stable. It is noted that the steeper the stratification, the more stable the ocean. This is because the higher stratification means that more potential energy need to be overcome by a parcel of water to travel vertically. This energy can be supplied by wind stress or internal turbulences.
In saline water (salinity > 1000 ppm) water is in its densest form when below zero degrees. However, salinity and the temperature and pressure distributions determine the level of stratification. Stratification occurs when water masses with different properties form different small layers (<30m thickness) whose density increase with depth. These layers act as barriers to water mixing. The different properties of the water include salinity and temperature, and thus density. The salinity of the surface water is mainly determined by the balance between evaporation and precipitation. In the subtropics evaporation is clearly higher than precipitation, which leads to the highest surface salinity in these regions. The warmest surface water is in low latitudes due to the more direct sunlight in these regions.
Thermocline, Pycnocline and Halocline
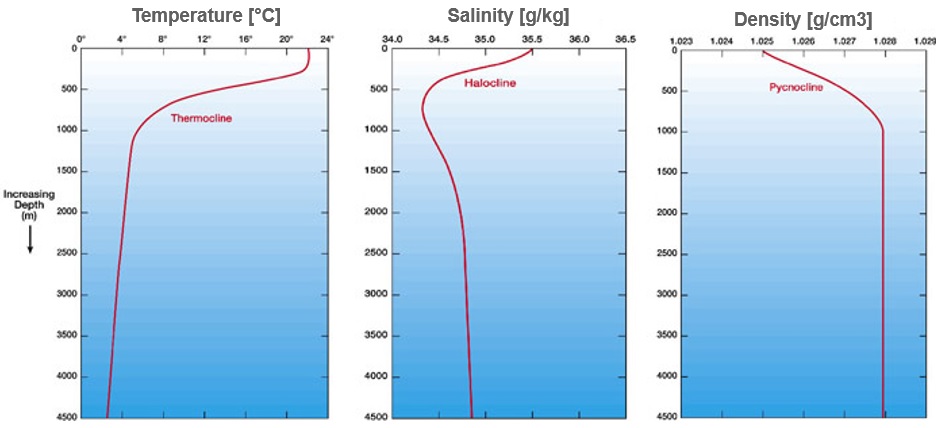
Three special features characterise the water, salt, and density curve in stratified ocean water: thermocline, pycnocline, and halocline.
These are explained in some detail below.
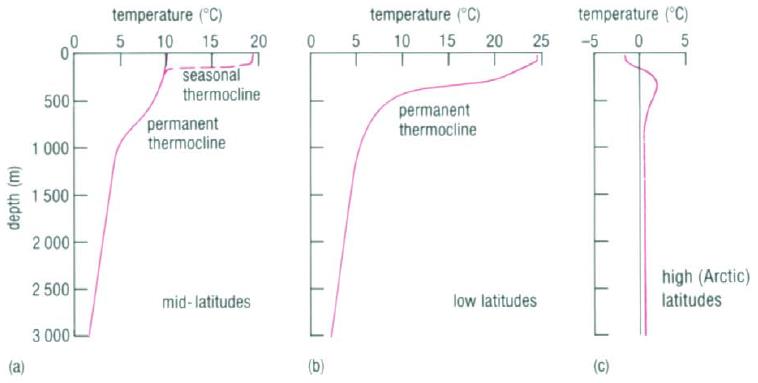
- A Thermocline is a layer in which the temperature profile is very steep. In low latitudes the temperature difference across a thermocline is in the order of 20°C. The thermocline is induced by the temperature-dependent density gradient. Thermoclines are steeper in shallow water. Furthermore, they are the sole reason for stratification in lakes, where haloclines do not exist.
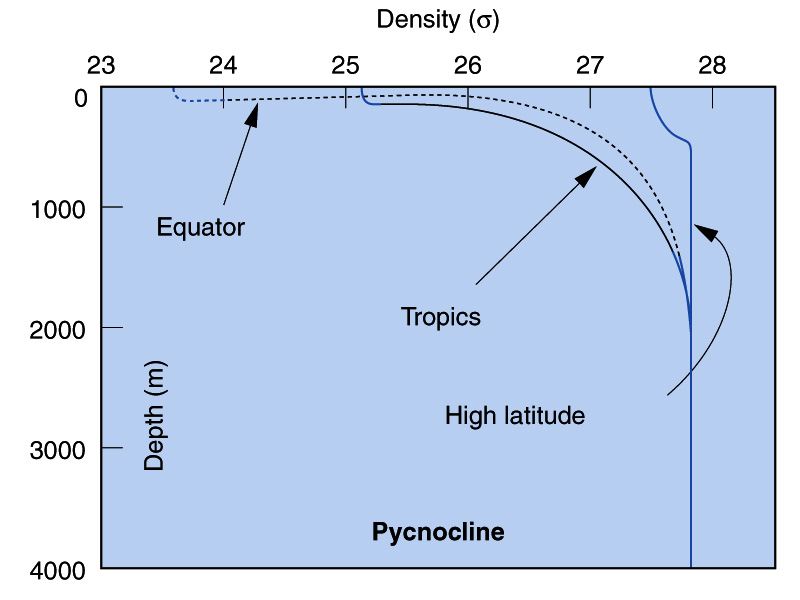
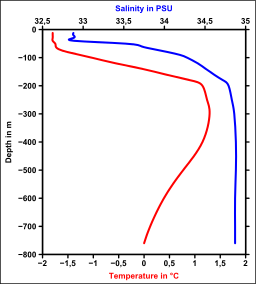
- Pycnoclines are regions in which density increases rapidly with depth. In a pycnocline water is necessarily very stable (ie. it would take a huge amount of energy to displace the water mass up- or downwards). Pycnoclines are generally much more distinctive in low latitudes (see image).
- Haloclines are consequently layers in which the salinity gradient is unusually steep. Fresh water does not mix with deep ocean water in this zone. This may occur if the fresh water is not cold enough to go beneath the sea water. Haloclines are often located in the mid and low latitudes, since in higher regions fresh water is mostly cold enough – it often comes from molten ice. The high latitudes are, however, also the regions in which deep water formation occurs, which demands for the mixing of cold, fresh and warmer, salty water.
Buoyancy Frequency
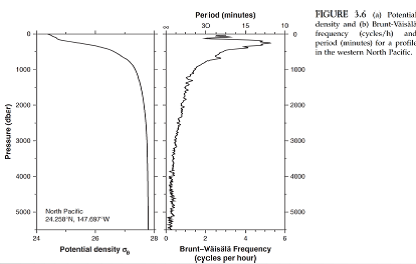
Another feature in stratified water is the buoyancy frequency, which is directly associated with static stability. In a stably stratified water a water parcel may be displaced upwards, but due to it being denser, and hence heavier, than its new surroundings it will sink and due to inertia overshoot its initial position. However, beneath the original position the water around the parcel is denser and the parcel will be forced upwards again.
This process is repeats indefinitely resulting in an oscillation. Consider a small parcel of water of Volume $V$ and density $ \rho $ in an environment in which a density that is a function of height: $\rho = \rho (z)$. If the parcel is displaced by a vertical increment $z'$, it will be subject to an extra gravitational force $F_g$ against its surroundings of:
$$ F_g = - g \rho (z) V +g\rho (z+z') V $$
By Newton's law $ F = m a$ the parcel will be accelerated. With $m=\rho_0 V$ and $a=\frac{d^2 z'}{dt^2}$ one obtains after dividing by $V$ the differential equation
$$\rho_0 \frac{d^2 z'}{dt^2} = -g (\rho(z) + \rho (z+z'))$$
Here $g>0$ is the gravitational acceleration. For a small displacement one can approximate $\rho (z+z') - \rho (z) \approx \frac{\partial \rho (z)}{\partial z} z'$ which lead to
$$\frac{d^2 z'}{d t^2} = \frac{g}{\rho_0} \frac{\partial \rho (z)}{\partial z} z' $$ For stable stratification $\frac{\partial \rho (z)}{\partial z} < 0$ the solution of this ordinary differential equation has the solution
$$z' = z'_0 \cos (Nt) $$,
where $N$ is the the buoyancy frequency:
$N = \sqrt{- \frac{g}{\rho_0} \frac{\partial \rho (z)}{\partial z}}$.
Sources
- Open University, 1995, Seawater: Its Composition, Behaviour and Properties
- Wikipedia.com, online on: http://en.wikipedia.org/wiki/Thermocline, letzter Zugriff: 5.3.2014
- Wernli, Heini et Pfahl, Stephan, 2013, Skript Umweltfluiddynamik (ETHZ)
- Fröhlicher, Thomas, 2013 Vorlesung: Physikalische Ozeanographie am 5.3.2014
- Wiktionary.org, online on: http://en.wiktionary.org/wiki/caballing, accessed on: 22.02.2015
- Eoearth.org, online on: http://www.eoearth.org/view/article/150812/, accessed on: 23.02.2015
- USGC Water Science School, online on: http://water.usgs.gov/edu/saline.html, accessed on: 25.02.2015
Comments
- I modified the second last sentence in the “Stratification”-section, the third sentence in the “Buoyancy Frequency”-section and I corrected the units for the buoyancy frequency… — Laura Arnold 2014/04/16 14:44
- Please revise last paragraph “Buoyancy Frequency” (see lecture slides) — Alexander Haumann 2014/07/01 11:12
- I edited the last sentence in “Buoyancy Frequency” — Leonardo Echeverria
- Added definitions of stratigraphy and caballing. Gave reasons for warmer surface temperature in low latitudes. Expanded section on buoyancy frequency; adding the cause of higher buoyancy frequency, and a definition (incl. mention of the Brunt – Väisälä frequency). Changed saline water limits from <20ppm to <1000ppm. Edited general grammar of article. Wanted to add diagram from lecture 2 of thermocline, pycnocline, and halocline, but the webpage would not let me upload a picture. Would like to check stratigraphy thickness of <30m (could not find any source to confirm this). — Emma Velterop 2015/02/25 11:47