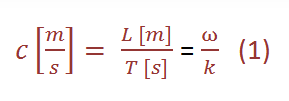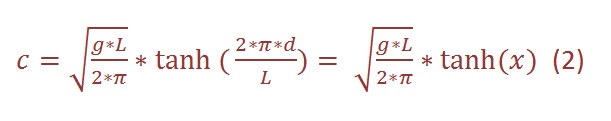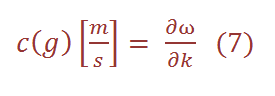Author: Hannah Wey

1. Phase velocity

A wave transfers energy from one part of a material to another, in this case in a water body. Important terms related to waves are

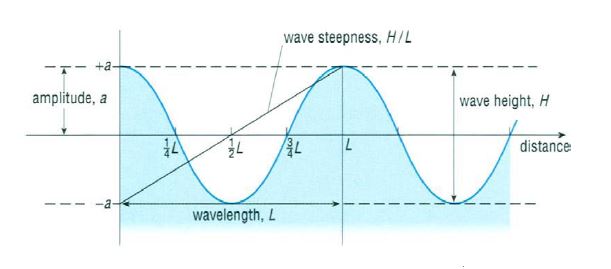
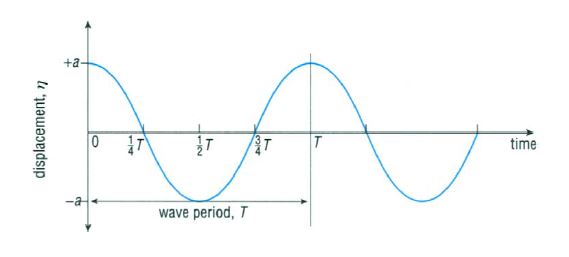
wave height H [m]
wavelength L [m]
period T [s]
phase velocity c or c(p) [m/s]
group velocity c(g) [m/s]
wave number k [m-1] = 2π/L
angular frequency ω [s-1] = 2π/T = c*k
amplitude a [m]
frequency f [s-1] = 1/T 

The four first terms can be seen in figures 1 at the left (displacement versus distance, time is constant) and figure 2 at the right (displacement versus time, place is constant) and are important for the following chapter.

The phase velocity can be expressed as

←- phase velocity in general

which is simply a form of the well-known expression: speed = distance / time. Further, and a little bit more complicated, the velocity of a wave can be described as

←- phase velocity in general

where d[m] is the depth of the water body (in the lecture is was declared as H). When x is small, then tanh(x) = x, and if x is larger than π, then tanh(x) = 1. Therefore, we can differ between deep and shallow water. In the latter case, when the depth and therefore x are small, the velocity can be written as

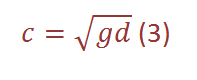←- phase velocity in shallow water

It can be seen that this velocity depends on the depth due to an interaction with the sea-bed, namely the friction.

In deep water, where x is big, the water velocity results in

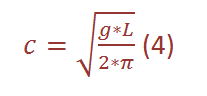←- phase velocity in deep water

Here, friction and therefore the depth of the water body can be neglected. It is possible, given only one of the wave characteristics c, T or L, to calculate either of the other two: With (1) and (4) the following expressions can be derived:

←- deep water

2. Group velocity

The group velocity is the speed of the envelope of the waves. Mathematically, it is defined as

The function ω(k), which gives ω as a function of k, is known as the dispersion relation. The group velocity therefore depends on this function, what is shown in the following movie. If ω is directly proportional to k (ω = ak), then the group velocity is exactly equal to the phase velocity. If ω is a linear function of k, but not directly proportional (ω = ak+b), then the group velocity and phase velocity are different. The envelope of a wave packet will travel at the group velocity, while the individual peaks and troughs within the envelope will move at the phase velocity.

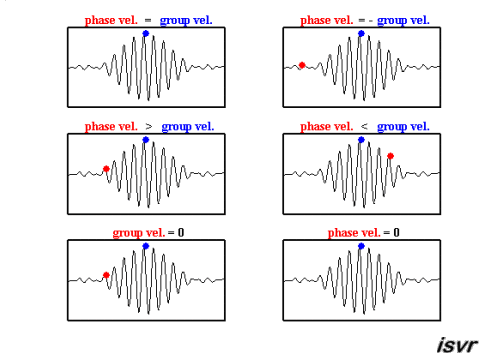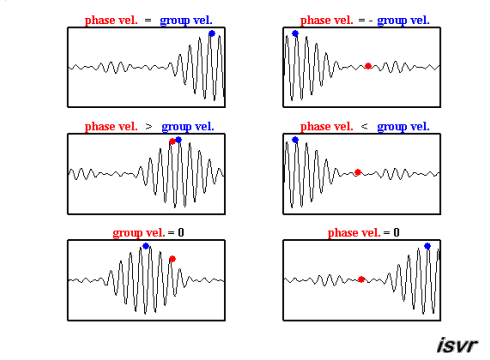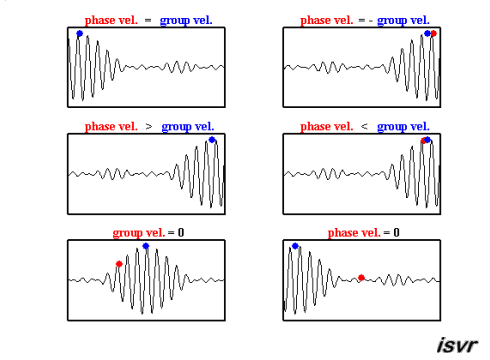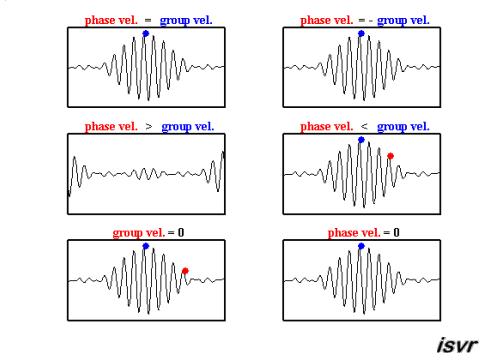(source: http://resource.isvr.soton.ac.uk/spcg/tutorial/tutorial/Tutorial_files/Web-further-dispersive.htm)

Again, deep and shallow water waves have to be discussed seperately, as it is assumed that shallow water waves are non-dispersive, in contrast to deep water waves: It is shown in the table at the end that the group velocity in deep water is half the phase velocity and in shallow water, the group velocity equals the phase velocity.

←- derivation of the group velocities in deep and shallow water

---