Author: Laura Arnold

The coriolis force is a fictitious force which only occurs from the reference point of a rotating framework. On the rotating Earth, we are on such a reference framework and the coriolis force has important effects on large scale motions (The influence on the ocean).

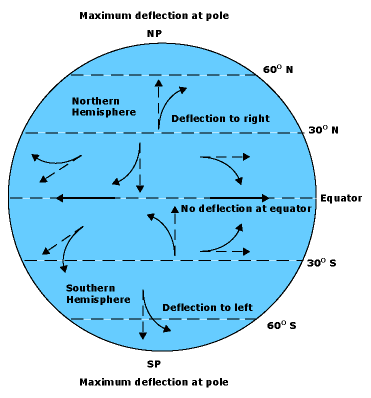
The coriolis force acts at right angles to the direction of motion. It causes a deflection of a moving particle to the right on the northern hemisphere and to the left on the southern hemisphere. The reason for this is that a parcle at the equator has a relatively high tangential velocity of rotation as it is far away from the Earth's axis of rotation (tangential velocity = angular velocity $\cdot$ the distance from the axis of rotation). At higher latitudes the tangential velocity of a parcel on the Earth is slower than at the equator as its distance to the axis of rotation is smaller. Now, when a parcel moves from the equator towards the north pole for example, its higher tangential velocity compared to the parcels with lower tangential velocity further in the north seems to displace it towards the right. The effect can be seen in Figure 1 and it is also shown in this movie: Deflection due to the coriolis force

Figure 1: The effect of the coriolis force (National Snow and Ice Data Center, 2014)

Also indicated in Figure 1 is that the coriolis force has no effect at the equator. The magnitude of the coriolis force is proportional to its velocity and decreases with decreasing latitude (compare with the value of the coriolis parameter f explained below).

If it is mathematically accounted for having a rotating reference framework, two additional terms add to the momentum equation for an inertial framework of reference (see "vector transformation" on slide 12 for a mathematical derivation). These two terms stand for the centrifugal force and the coriolis force.

The centrifugal force is counteracted by the gravitational force and can be accounted for by adjusting the net gravitational term according to the location on the Earth’s surface (Cushman-Roisin & Beckers, 2011).

The coriolis acceleration is described by:

\begin{equation*} 2 \vec{\Omega} \times \vec{u} \end{equation*}

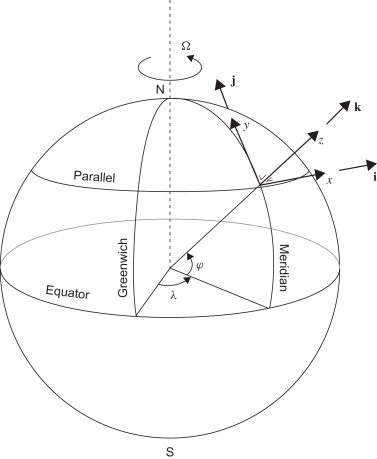
$\vec{u}$: the velocity vector, $\begin{equation*}\vec{u}=(u,v,w)\end{equation*}$ , with u: the velocity in x-direction, v: the velocity in y-direction, w: the velocity in z-direction (see Figure 2)
$\vec{\Omega}$: the angular velocity of the Earth, with $\begin{equation*}\Omega = \frac{2\pi}{24 hours} \cong 7.29\cdot10^-^5 s^-^1\end{equation*}$.

This is equal to:

$\begin{equation*}2\Omega\cdot(0,\cos\varphi,\sin\varphi)\times\vec{u}\end{equation*}$ ,with $\begin{equation*}2\Omega\cdot\sin\varphi=f\end{equation*}$

$\varphi$: the latitude (see Figure 2),
$f$: the coriolis parameter with a value of $\begin{equation*}2\Omega\cdot\sin{45^\circ}=\frac{2\Omega}{\sqrt{2}}\cong10^-^4 s^-^1\end{equation*}$ at mid latitudes (45° north). In the southern hemisphere the coriolis parameter is negative.

$\begin{equation*}2\Omega\cdot\cos\varphi\end{equation*}$ can be neglected, what leads to the coriolis force

$\begin{equation*}2\vec{\Omega}\times\vec{u}=2\Omega\cdot(0,\cos\varphi,\sin\varphi)\times\vec{u}\cong(0,0,f)\times(u,v,w)=(-fv,fu,0)\end{equation*}$.

Figure 2: Framework of reference on the Earth (Cushman-Roisin & Beckers, 2011)

Thus the momentum equation in vector form for a rotating framework of reference is: \begin{equation*}\frac{D\vec{u}}{Dt} + 2\vec{\Omega} \times \vec{u}= - \frac{1}{\rho}\vec{\nabla}p + \vec{g} + \frac{\vec{Fr}}{\rho}\end{equation*}

(Münnich, 2014; Cushman-Roisin & Beckers, 2011; Brown et al., 2001).

The coriolis force has an effect on several large scale motions in the ocean. E.g.:

• inertia currents:

These are curved ocean currents (see Figure 3) on which no real force acts. This can happen when a wind ceases to blow until friction finally stops the motion.In this case, the coriolis force operates as a centripetal force, what causes the circular pattern (Brown et al., 2001). This feature can be seen in Figure 4.

Figure 3: inertia currents in the ocean (Stewart, 2005)

Figure 4: the coriolis force acting as a centripetal force causing circular motion (University Blog, 2011)

• geostrophic flow → geostrophy

• Ekman transport → ekman

• Cushman-Roisin,B.; Beckers,J.-M. (2011), The Coriolis Force, in: Introduction to Geophysical Fluid Dynamics, Physical and Numerical Aspects, Volume 101, Chapter 2, pg.: 41-75
• Brown,E.; Colling,A.; Park,D.; Phillips,J.; Rothery, D.; Wright, J. (2001), Ocean Circulation (Second Edition), Open University, Elsevier Ltd., pg.: 37-78
• Münnich, M., Lecture: Introduction to Physical Oceanography, wind-driven circulation I, 9 April 2014
• National Snow and Ice Data Center (2014), from: http://nsidc.org/cryosphere/arctic-meteorology/factors_affecting_climate_weather.html [15.04.2014]
• http://www.youtube.com/watch?v=mcPs_OdQOYU [09.04.2014]
• Stewart,R.H. (2005), Chapter 9 - Response of the Upper Ocean to Winds, from: http://oceanworld.tamu.edu/resources/ocng_textbook/chapter09/Images/Fig9-1s.jpg [23.04.2014]
• University Blog (2011), Inertia Currents, from: http://2.bp.blogspot.com/-ZVvbBrV1H50/Tk9Tf1_3KnI/AAAAAAAAAG0/-uYICGXmbns/s1600/inertia+current+motion.png [23.04.2014]